计算机图形学-纹理
概述
纹理映射是着色部分的内容,包括了抗混叠等技术。
重心坐标 Barycentric Coordinates
重心坐标是定义在三角形上的,表示为\((\alpha, \beta, \gamma)\),满足:
\[ (x, y) = \alpha A + \beta B + \gamma C \\ \alpha + \beta + \gamma = 1 \] 当点在三角形内时,满足: \[ \alpha > 0 \wedge \beta > 0 \wedge \gamma > 0 \] 重心坐标可以通过面积比求出,如图
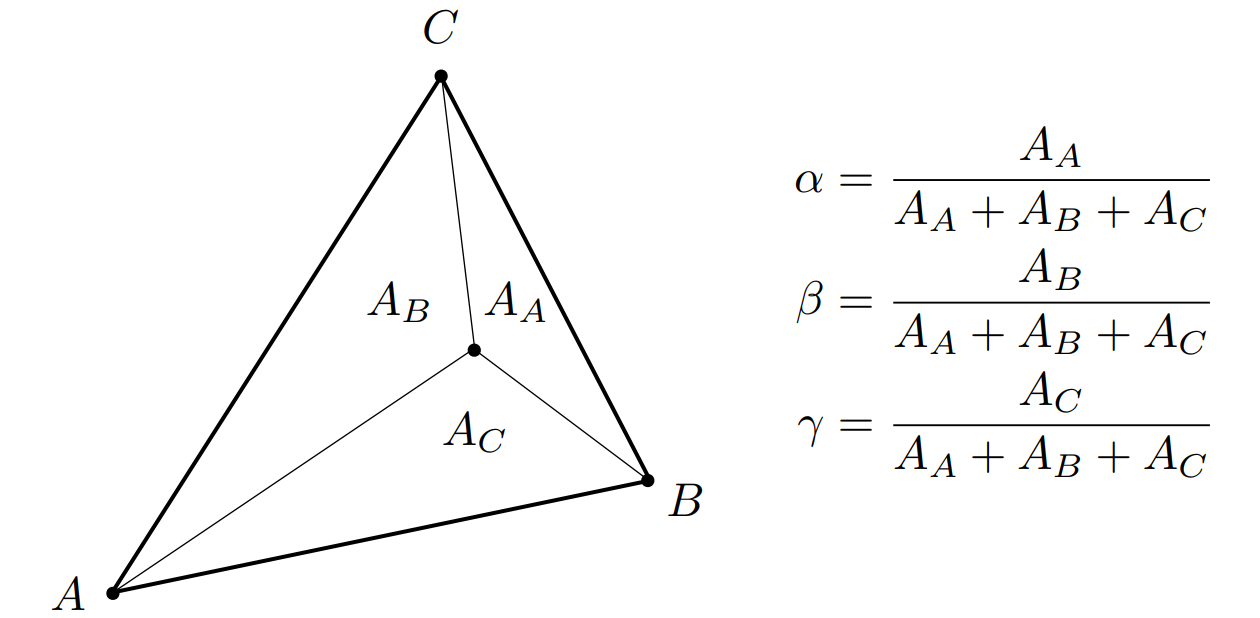
除了用面积算,还可以直接通过笛卡尔坐标系下的坐标进行计算

使用重心坐标进行插值
对需要插值的对象也用重心坐标的形式表示
重心坐标不能保证投影变换后坐标不变,所以对于深度信息等需要现在三维空间中插值,再投影到屏幕空间。
纹理映射
对于光栅化之后的点(u,v)进行纹理映射:texture.sample(u,v),采样得到的值可以替代Blinn-Phong反射模型中漫反射光照中的\(K_d\)参数,用来表示物体表面本来的颜色。
在纹理采样过程中会遇到一些问题:
纹理放大
计算机图形学-纹理
https://blog.scubot.com/article/ee3e/