计算机图形学-抗混叠

概述

本文致力于记录有关计算机图形学中抗混叠/反走样(anti-aliasing)的相关知识⛄。

混叠的产生

计算机图形学的光栅化就是屏幕对二维图像的采样，是一个连续到离散变化的过程。

在采样的过程中会产生错误的现象(Artifacts)：

• 锯齿(Jaggies)——空间采样

• 摩尔纹(Moire Pattern)——空间采样

  

• 货轮效应(Wagon Wheel Illusion)——时间采样

  

当采样的频率跟不上信号变化的频率时，就会产生Artifacts，也可以称作Aliasing-混叠/走样

傅里叶级数展开

任何的周期函数，都可以写成一系列正弦和余弦函数的线性组合与一个常数项的和。 \[ f(x)=A_0/2 + \sum_{n=1}^{+\infty} A_n\cdot \sin(2\pi nx /P + \phi_n) \] \(f(x)\)是周期为\(P\)的周期函数。

效果图：

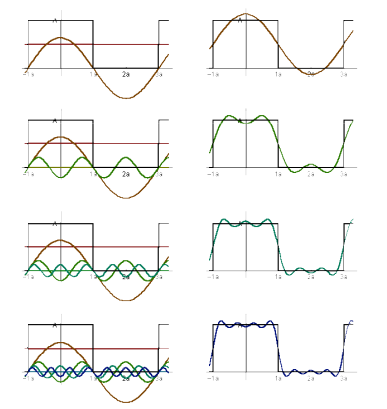
关于傅里叶级数更多的是介绍可以参考这篇文章，后续会补充傅里叶级数展开到傅里叶变换的过渡内容。

傅里叶变换与逆变换

傅里叶变换(Fourier transform)可以将信号从空域/时域(Spatial domain)转化到频域(Frequency domain)，傅里叶逆变换可以将这个过程反过来。

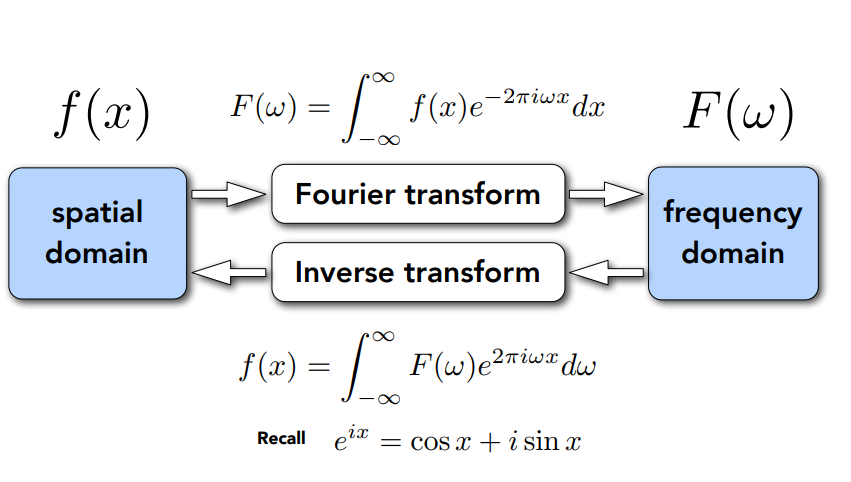
时域到频域变换的更直观的理解：

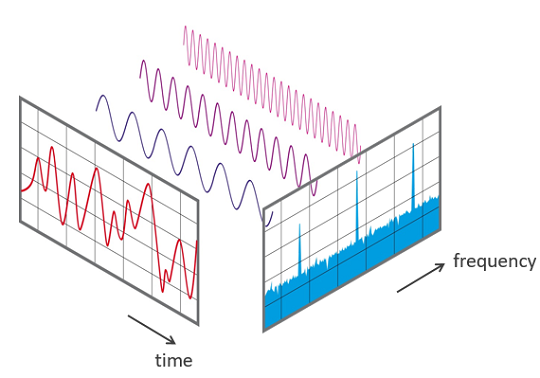
未完待续...