简单疏散模型(2019美赛)
概述
这一切要从2019MCM/ICM(题目下载地址)开始说起,我们小组拿到题目之后经过讨论选择了D题。这其实也是我个人的意向,因为今年的题目普遍需要生物和金融方面的知识,而我们组除了我是计科专业的,其他两位都是做理论物理方向,而今年的题目普遍没有物理发挥的余地,所以我尽量去找一些适合计科的题目。但B题C题给我的第一感觉就是只有我一个人写程序做数据处理肯定搞不定,所以我和小组都将目标放在了我有点思路的D题上。
D题说的是模拟卢浮宫中发生恐怖袭击的人群疏散情况,具体的题目就不详细说了,我这里详细介绍一下我在队友帮助下建立起的简单疏散模型。
模型设计
预处理
将实际的人群分布抽象成网络图,即每个点表示一个区域,连接两个点的边表示该两区域之间可以通行。
其中每个点和每条边都存有若干属性:
- 点:该区域目前的人数\(N\)和该区域能容纳的最大人数\(M_v\)。
- 边:该通道单位时间能通过的人数\(F\)和该通道单位时间能通过人数的最大值\(M_e\)。
最后将复杂的实际人群分布图抽象成一张简单图(simple graph),例如:
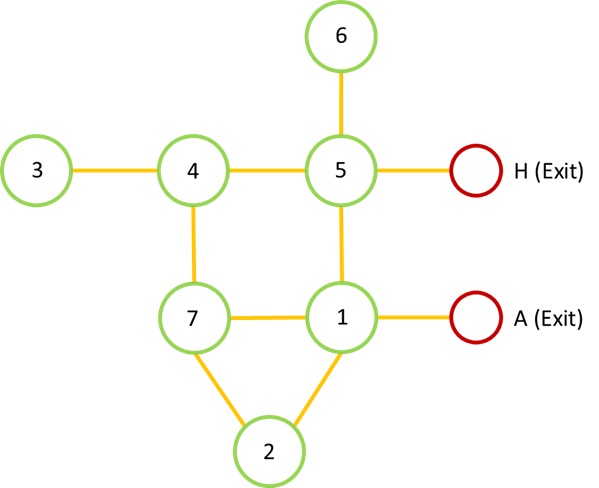
绿色结点表示有人群分布的区域
红色结点表示出口标志(不存信息)
要说明的一点是,与纯图论的图不同,这里抽象出的图结点与边都存有信息,而纯图论中只有边会存储信息,点是不存信息的。这是因为图论是研究关系的一门科学,边存储的信息用来表示两个量之间关系的程度(见每个图具体的定义),而点只作为标志。所以可以认为我们抽象出的图的边仍可叫做Edge,但结点由于存储有信息不如叫做Node而不用Vertex。
定义
我们的模型目的是去模拟在有多个出口且位置已知的情况下,不同结点在各个时间段的人群分布情况,进而获得全局的疏散情况。
因此,我们需要定义一些符号来解释这些逻辑。
| 符号 | 含义 |
|---|---|
| \(U_t\) | 单位时间 |
| $v_i $ | \(v_i = \{N, M_v\}\),标记为\(i\)的结点 |
| \(e(v_i, v_j)\) | \(e(v_i, v_j) = \{F_l, M_c, \epsilon\}\),连接\(v_i\)和\(v_j\)的边 |
| \(\delta\) | 单位时间内该结点人数的减少量 |
| $F_l $ | 某条边在单位时间内通过的人数 |
| $M_e $ | 某条边在单位时间内能通过的最大人数 |
| \(\epsilon\) | 人群对某条边的偏向程度 |
| \(N\) | 某一结点的人数 |
| $M_v $ | 某一结点能容纳的最大人数 |
| \(N^+(v_i)\) | 与\(v_i\)邻接且已经更新过的结点的集合 |
| \(N^-(v_i)\) | 与\(v_i\)邻接且未更新的结点的集合 |
| \(lt^T, lt^E, lt^D\) | 限制某个结点人数转移的三个限制因素 |
算法原理
首先我们认为\(\rightarrow\)代表引用集合中某个元素,例如\(v_i\rightarrow N\)表示$v_i $中的人数。
且规定\(v_i\rightarrow \delta = \min(lt^T, lt^E, lt^D)\)。也就是说只要知道那三个限制因素,就知道在单位时间内某个结点的人数变化。
为了更好地在计算机中处理数据,我这里对整个疏散过程离散化。也就是定义一个单位时间,在该单位时间内计算所有结点的人数减少量,即可反应该单位时间内的人数变化趋势,直到人数都为0为止,疏散完成。
在单位时间内,我这里用BFS的方法,以所有出口结点初始化BFS队列,然后向外扩散至每一个结点。
针对扩散到的某一结点\(v_i\),我们很容易就可以算出来\(N^+(v_i)\)和\(N^-(v_i)\)。接下来就要算那三个限制因素。
目标结点限制
假设我们处在某一结点上,前面有多个方向都发生了人数流动,且人数都在减少。该结点上的每一个人都会选择多个方向中的其中一个方向前进,由定义可知,\(v_i\)结点人数的流动一定是向\(N^+(v_i)\)中的结点的。
假如我们已经知道了\(v_i\)向\(N^+(v_i)\)中某个结点\(v_t\)的偏向性\(\epsilon\),即\(e(v_i, v_t)\rightarrow \epsilon, v_t \in N^+(v_i)\),那么:
\[ lt^T = e(v_i, v_t)\rightarrow \epsilon \times(v_t \rightarrow M_v - v_t\rightarrow N) \]
也就是说,该方向的偏向性乘上目标结点还可以容纳的人数就是该结点在该方向的结点取向限制 $lt^T $。
而某条边的偏向性\(\epsilon\)可以通过这样的公式得到:
\[ \forall v_k \in N^-(v_i) \ e(v_i, v_k) \rightarrow \epsilon \\[2ex]= \frac{\min(v_k\rightarrow N, e(v_i, v_k) \rightarrow F_l \times U_t)}{\sum_{v\in N^-(v_i)} \min(v\rightarrow N, e(v_i, v) \rightarrow F_l \times U_t)} \]
边流量限制
边所能承载的流量也是限制结点人数转移的一大因素。假设我们要从\(v_i\)向\(v_t\)转移人数,且\(v_t \in N^+(v_i)\)。
\[ lt^E = e(v_i, v_t) \rightarrow F_l \times U_t \]
该方向边的流量乘上单位时间即该结点在该方向的边流量限制\(lt^E\)。
特别地,边流量也可能随着时间的变化而变化,影响其变化的主要因素就是起点与终点的人数差。人数差越大,边流量也就越大,反之亦然。表示为:
\[ e(v_i, v_t) \rightarrow F_l \propto \mid v_i\rightarrow N - v_t \rightarrow B\mid \]
结点偏向性限制
当人群有多种出口选择的时候,人们会偏向选择流动最快的。但是在紧急疏散过程中,根据人群的从众心理,很有可能在有多种选择时,人们偏向选择人数多方向。即在向目标结点转移限制的表示为:
\[ lt^D = v_i \rightarrow N \times \frac{v_t \rightarrow N + v_t \rightarrow \delta}{\sum_{v\in N^+(v_i) }v_t \rightarrow N + v_t \rightarrow \delta} \]
即多个目标方向中,人数越多的,该结点向目标结点的偏向性越大,即结点的偏向性限制\(lt^D\)。
模型测试
输入
仍然用预处理中的图片作为输入,再加上每个结点的相关信息。
结点信息
| 标签 | 是否出口 | \(N\) | \(M_v\) |
|---|---|---|---|
| 1 | false | 1600 | 3000 |
| 2 | false | 2000 | 3000 |
| 3 | false | 2500 | 2500 |
| 4 | false | 3000 | 3000 |
| 5 | false | 2600 | 3000 |
| 6 | false | 3000 | 3000 |
| 7 | false | 4000 | 4000 |
| A | true | NA | NA |
| H | true | NA | NA |
边值信息
| 结点编号 | 结点编号 | \(F_l\) | \(M_e\) |
|---|---|---|---|
| 1 | 2 | 6 | 10 |
| 1 | 7 | 4 | 10 |
| 1 | 5 | 3 | 10 |
| 1 | A | 5 | 10 |
| 5 | H | 7 | 10 |
| 5 | 6 | 3 | 10 |
| 5 | 4 | 2 | 5 |
| 4 | 7 | 3 | 5 |
| 2 | 7 | 4 | 5 |
| 3 | 4 | 6 | 10 |
输出
经过程序模拟,得到疏散的过程,我们把数据放到MATLAB中进行数据的可视化,得到结果:
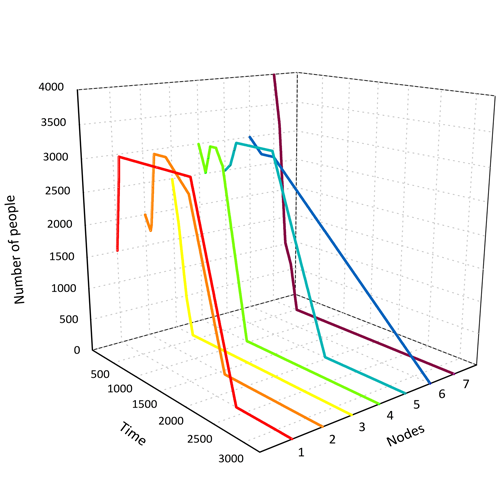
结果就如看到的这样,每个结点的人数随时间的变化趋势。
分析总结
其实在比赛中的模型内容比上面说的要复杂一些,但是总体的思路并没有变。当时在设计的过程中抛弃了很多想法,原因很简单,我一个人能力达不到或者是时间不够用。
也就是在美赛的第一天下午我们就商量决定用这种方法去构建模型,在程序设计的过程中我也遇到了很多细节问题,针对这些问题我自己做了一些决策,不过至少跑出来了结果。
如果要我分析这个算法,我是很不愿意的。因为我知道这个算法就是一个离散时间跑多次BFS再加上四个我拍脑袋想出来的数学公式,它基本没有使用价值,存在的意义仅仅是帮我完成论文和锻炼我的编程能力。
但是毕竟这个模型也投入了我很大的精力,所以我才想写篇博客把这些内容记录下来,也希望我下次打数模比赛的时候多想想这次的教训,希望以后我能做得更好吧。