外部排序及性能测试

概述

文章以DSAA课程中的一个实验题目为例，展示:

具体算法细节(外部排序算法)
数据结构实现(数据结构)
程序性能测试(性能测试)

最后对实验的结果做分析与总结(程序分析)，再写一些感想(结语)。

这个实验课题的程序我连续肝了两天，其中最后一天在Wakatime上的记录coding时长突破了我一天写代码时长的记录达到10h。

最后一节DSAA课的时候(半个月前)也上台展示了自己的程序，不过现在想想有很多遗憾的地方，具体的在最后一部分总结时说。

写程序是一方面，测程序是另一方面。为了测试程序的性能，我在最后期末考试的复习阶段几乎把每科的复习时间压缩到了一天时间内，也写了一部分脚本花了很多时间进行反复测试。

所以

如果读者不太清楚外排的细节以及其性能的规律，不妨耐心看完，看到最后一定会有所收获；

如果读者已经对这部分内容了如指掌，也请多多指出文章内容的不合理之处以便我改正。

题目要求

下面是题目的具体要求:

For this task, you will implement an external sorting algorithm. The input data file will consist of 8N (N is a positive integer number) blocks of data, where a block is 4096 bytes. Each block will contain a series of records, where each record has 8 bytes. The first 4-byte field is a non-negative integer value for the record ID and the second 4-byte field is a float value for the key, which will be used for sorting. Thus each block contains 512 records.

Your job is to sort the file (in ascending order of the key values), as follows: Using replacement selection, you will sort sections of the file in a working memory that is 8 blocks long. To be precise, the heap will be 8 blocks in size; in addition you will also have a one block input buffer, a one block output buffer and any additional working variables that you need. To process, read the first 8 blocks of the input file into memory and use replacement selection to create the longest possible run. As it is being created, the run is output to the one block output buffer. Whenever this output buffer becomes full, it is written to an output file called the run file. When the first run is complete, continue on to the next section of the input file, adding the second run to the end of the run file. When the process of creating runs is complete, the run file will contain some number of runs, each run being at least 8 blocks long, with the data sorted within each run. For convenience, you will probably want to begin each run in a new block. You will then use a multi-way merge to combine the runs into a single sorted file. You must also use 8 blocks of memory used for the heap in the run-building step to store working data from the runs during the merge step. Multi-way merging is done by reading the first block from each of the runs currently being merged into your working area, and merging these runs into the one block output buffer. When the output buffer fills up, it is written to another output file. Whenever one of the input blocks is exhausted, read in the next block for that particular run. This step requires random access (using seek) to the run file, and a sequential write of the output file. Depending on the size of all records, you may need multiple passes of multiway-merging to sort the whole record. Your program will take the names of two files from the command line, like this:
1
extsort <record file name> <statistics file name>
The record file is the input data file to be sorted. At the end of your program, the record file (on disk) should be sorted. So your program does modify the input data file. Be careful to keep a copy of the original when you do your testing. In addition to sorting the data file, you must report some information about the execution of your program (e.g., the number of runs, and the time taken to sort the record file), which will be stored in the statistics file. If the specified record file does not exist, output a suitable error message and exit. Your program will create the statistics file if it does not already exist, or append to it if it does.

翻译成中文，简而言之：

定义内存中每个块的大小为4096 bytes(4 kb)。
待排序文件(为了简便下面统称为REC.dat)中只包含记录，且文件占8N个块大小(即32N kb)。
每条记录包含一个键(float类型, 4 bytes)和一个值(unsigned int类型, 4 bytes)，每条记录占8 bytes，以二进制方式存储，即每个块中正好能存下512条记录。
主存(main memory)允许10个块大小，其中：
- 1个块实现输入缓冲区
- 1个块实现输出缓冲区
- 8个块实现数据处理
用置换选择的办法按键的升序产生顺串，每一个顺串补全整数个块大小，所有的顺串首尾相接存储在一个顺串文件(统称RUNFILE.tmp)中。
用八路归并的方法归并顺串，最后得到的结果存储在REC.dat中，且保留一份原REC.dat的拷贝文件(统称cp_REC.dat)。
以追加的方式将排序的中间信息写入统计文件(统称STAT.csv)中。写入的信息至少包括：
- 置换选择产生的顺串的个数
- 排序所用的时间

分析与准备

首先要考虑的是待排序文件要怎么得到，我选择了用随机数随机产生数据得到数据文件，源码很简单如下：

random_creater.cc

#include <iostream>  
#include <fstream>  
#include <cstdlib>  
#include <string>  
#include <ctime>  
#include <cstring>  
using namespace std;

int N;
string filename;

const int maxn = 1e6;
const int block_rec = 512;

int main(int argc, char *argv[]) {
    srand(time(NULL));
    filename = argv[1];
    N = atoi(argv[2]);
    
    ofstream outFile(filename.c_str(), ios::out | ios::binary);
    if (!outFile.good()) {
        cout << "file open error!" << endl;
        exit(-1);
    }
    
    int total_ = block_rec * 8 * N;
    for (int inc = 0; inc < total_; inc ++) {
        pair<float, unsigned int> rec(1.0 * (rand() % maxn) / 11, rand() % maxn);
        outFile.write((char *)&rec, sizeof(rec));
    }

    cout << "_____________________________________________________" << endl;
    cout << "Succeed in writing 8 * 512 * " << N << " = " \
        << 8 * 512 * N << " records in file: " << filename << endl;
    cout << "File's size should be " << 8 * 4096 * N << " bytes" \
        << " (" << 32 * N << " kb)" << endl;
    cout << "_____________________________________________________" << endl;
    
    outFile.close();
    return 0;
}

调用方式(git bash)：

1	`$ ./random_creater.exe REC.dat N`

其中REC.dat为要产生的数据文件，N就是题目要求中的N，用来规定数据规模。

效果如下：

检查生成文件大小：

与目标一致。

其次就是怎么检查文件是否排序完成。由于所有记录以二进制方式存入，用文本编辑器打开会显示乱码，且记录条数达到$512\times8N$，所以需要用程序辅助检查。

我这里用简单的顺序查找方式来找出不符合键是升序这一要求的记录，如果查找完毕没有不符合要求的记录则认为文件已排序。源码如下：

check_sorted.cc

#include <iostream>  
#include <fstream>  
#include <cstdlib>  
#include <algorithm>  
#include <string>  
using namespace std;

string filename;  
string statFile;

int main(int argc, char *argv[]) {
    filename = argv[1];
    ifstream inFile(filename.c_str(), ios::binary);  
    if (!inFile.good()) {
        cout << "file open error" << endl;
        exit(-1);
    }

    pair<float, unsigned int> rec;
    double prec = -1e7;
    int idx = 0;

    while (inFile.read((char *)&rec, sizeof(rec))) {
        if (rec.first < prec) {
            cout << "__________________________________" << endl;
            cout << "file: " << filename << " has not been sorted" << endl;
            cout << "prev-idx: " << idx - 1 << "  key: " << prec << endl;
            cout << "curr-idx: " << idx << "  key: " << rec.first << endl;
            cout << "__________________________________" << endl;
            inFile.close();
            return 0;
        }
        prec = rec.first;
        idx ++;
    }

    cout << "file: " << filename << " has been sorted" << endl;
    cout << "__________________________________" << endl;
    inFile.close();
    return 0;
}

调用方式(git bash)：

1	`$ ./check_sorted.exe REC.dat`

我们来查一下刚刚随机生成的数据文件的有序情况(大概率下是没有排好序的，有兴趣的话可以去考虑计算一下记录非升序的第一个索引的期望)

很明显，该随即数据的文件并没有被排序，且第一处出现非升序的索引是prev-idx: 0。

接下来考虑外部排序的内容。

算法和数据结构下面两部分详细讨论，这里考虑STAT.csv中存储的数据内容。
- 待排序文件的大小，文件中记录的个数
- 产生的顺串总个数
- 八路归并的次数
- 产生顺串消耗的时间
- 归并消耗的时间
- 总消耗的时间
只需要在排序过程中记录以上数据，最后再输出到文件。

外部排序算法

说明

外部排序是指对大型文件的排序算法，由于无法将文件内容全部读入到主存中，所以一般采用产生顺串再归并顺串这样的归并排序算法的思想。

外部排序与内部排序的最大不同就是，制约算法效率的核心因素不同。

内部排序制约算法效率的核心因素是数据比较/交换的次数(桶排序，基数排序等除外)
外部排序制约算法效率的核心因素是读取和写入文件的次数

外部排序是一类算法，具体的实现也不尽相同，这里实现的算法只是其中一种。不过不论哪一种外部排序算法，其核心思想都是将对文件的I/O操作次数降到最小，具体体现为利用特定的算法，使得产生的顺串个数尽可能小，这也是产生顺串的过程采用置换选择的原因。

对所有置换选择产生的顺串进行归并，一般采用多路归并。考虑到主存空间及时间效率等限制，采用八路归并。

流程图

程序流程

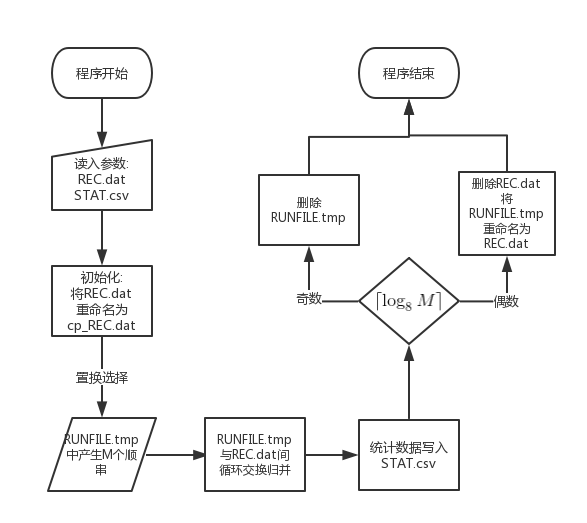
置换选择

置换选择(Replacement selection)是用来产生顺串的一种算法，其本质是最小堆的变形。

算法流程

从文件中读取数据，读到最小堆的数组里，这里根据要求读入8个块大小。记录最后一组数据的索引为$LAST=8\times 512 -1$。
利用数据中键的偏序关系建立最小堆。
重复以下步骤直到最小堆为空($LAST < 0$)：
1. 取出堆顶数据送到输出缓冲区。
2. 从输入缓冲区读入一组数据$R$，将其放置在堆顶。
3. 如果$R$比刚刚输出的堆顶数据小，则将$R$与堆中索引为$LAST$的数据交换位置，之后$LAST=LAST-1$。
4. 对堆顶数据进行下沉(Sift down)操作。
上一步完成后就产生了一个顺串，这时只需重复<2>和<3>直到输入缓冲区为空停止。

算法框架

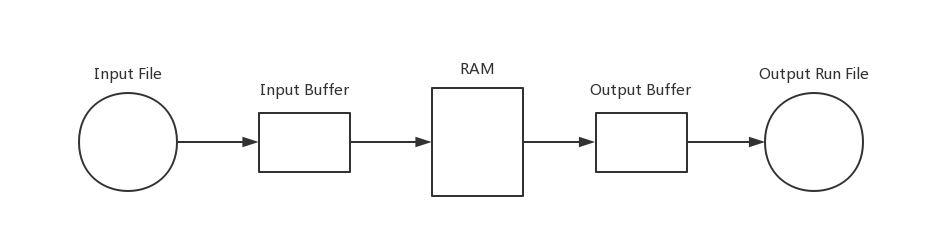
算法分析

堆的容量为$8 \times 512$，在平摊意义下每个顺串包含的数据个数为为$2\times8\times 512$。

若有$8\times512N$条记录，最后的顺串个数约为$\frac{8\times 512N}{2\times 8\times 512}= N /2$。

多路归并

以八路归并为例子，将产生的多个顺串归并到一个文件中。

由于归并路数不大，我们可以直接顺序搜索8个元素中最大的那个。

例如：

现在一共有$M$份顺串，我们将他们在文件$A$和$B$间进行归并：

首先将$M$每8个分成一组，最后多出来的可能不够8个。
构造一个输入缓冲池(8个块)，由8个输入缓冲区构成，每个缓冲区负责读入一份顺串。
每个输入缓冲区取出一份记录，在8条记录中找到最小的那份送到输出缓冲区。
一旦有输入缓冲区为空就继续读入文件，直到该文件读完该缓冲区搁置。
一旦输出缓冲区为满则向输出文件$A$中输出。

每组顺串重复以上过程直到结果全部输出到$A$。所以我们能在该文件中得到$\lceil \frac{M}{8}\rceil$个顺串。

然后对$A$中的顺串进行同样过程的归并，得到的顺串输出到$B$，再经过同样的过程输出到$A$。直到顺串个数为1。

所以我们得到八路归并$M$条顺串的文件操作次数是$\lceil \log_8M\rceil$次。

数据结构

上面的内容更偏重理论的分析，这部分我们将着手于在C++中的算法实现。

由于篇幅有限，接下来我给出一些设计思路于关键类的定义与说明，具体实现部分还请参考External-sorting。

类定义：缓冲区

根据题目的具体要求，程序需要进行多次文件操作，也是我们出于对主存利用效率更高的需求，程序中需要实现对输入输出缓冲区的模拟。故有Buffer类定义：

class Buffer {
public:
    Buffer();
    ~Buffer();
    // 从参数指定的文件输入流中的指定参数字节位置开始读入一个缓冲区大小的数据
    bool get_input(std::ifstream &, int = -1); 
    // 向参数指定的文件输出流中以二进制输出整个缓冲区内容
    bool write_output(std::ofstream &);
	
    // 获得当前__curr索引下的记录 
    // typedef std::pair<float, unsigned int> pis;
    pis get_value();
    // 获取当前__curr索引
    int get_curr();
    // 向缓冲区末尾追加新纪录
    void append_value(pis);
    void move_to_start();
    void move_to_end();
    void move_to_next();

    void clear();  // 清空缓冲区

    bool at_end(); // 判断是否读到末尾
    bool empty();  // 判断缓冲区是否为空
private:
    pis __buffer[rec_max];  // 缓冲区数组定义
    int __curr;  // 当前记录索引
    int __maxN;  // 当前缓冲区的记录数目
    bool is_empty;          // 是否为空
};

类定义：最小堆

支持置换选择算法的数据结构是最小堆的变体，下面给出最小堆Min_heap的类定义：

class Min_heap {
public:
    Min_heap();
    ~Min_heap();
    // 根据缓冲区和文件输入流参数初始化最小堆中的值
    void init(Buffer &, std::ifstream &);
    // 是否为空堆
    bool empty() const;
    // 关键函数，用来实现置换选择算法
    pis remove_add(pis);
    // 建堆
    void build_heap();
    // 当前堆大小
    int  size() const;
private:
    int __left(int) const;
    int __right(int) const;
    bool __isLeaf(int) const;
    // 下沉
    void __siftdown(int);
    // 最小堆数组
    pis heap[block_num * rec_max];
    int __maxN;
    int __curr;
};

类定义：外部排序管理

整合外部排序算法，定义对外接口函数，使排序实现更简洁。

给出Extsort_Manager类定义：

class Extsort_Manager {
public:
    // 读入argv参数
    Extsort_Manager(char **);
    ~Extsort_Manager();
    // 初始化
    bool init();
    // 置换选择建立顺串
    void create_runfile_RS();
    // 顺串八路归并
    void merge();

private:
    void __merge(int, std::vector<pii> &);

    std::string rec_fname;  // 待排序文件名
    std::string stat_fname; // 信息统计文件名
    std::string run_fname;  // 临时顺串的文件

    std::ifstream inFile;
    std::ofstream outFile;
    std::ofstream statFile;
    // 记录临时顺串的索引信息
    std::vector<pii> run_idx;
    
    Buffer input_buffer; // 单独的输入缓冲区
    Buffer output_buffer; // 单独的输出缓冲区
    // 归并中用到的输入缓冲池
    Buffer buffer_pool[block_num];
    // 最小堆
    Min_heap min_heap;
    // 实现计时功能
    std::clock_t start_clc;
    std::clock_t run_build_cost;
    std::clock_t merge_cost;
};

性能测试

外部排序程序实现之后我们需要对其进行测试。

测试概况

由于还需要进行多组的测试，所以check_sorted.exe将检查结果同样写入STAT.csv文件中，同样对random_creater.cc进行一部分修改。

特别的，由于测试数据来源是完全随机的，很难避免测试结果的偶然性，所以我们采用多次测试结构取平均值的方法对某一个N值进行测试。

为了更方便进行多组测试，我们利用shell脚本对测试逻辑打包，具体如下：

autoTest.sh

########### 测试开始 ############
echo "-----info-----"     # 输入信息块
recFile="REC.dat"         # 为了方便测试，规定待排序文件名称
read -p "input statfile: " statFile  # 输入信息统计文件名称
read -p "input minN: " minN          # 最小的N
read -p "input maxN: " maxN          # 最大的N    满足 minN <= N <= maxN
read -p "input step: " step          # N自增的步长  及每次循环N自增的数值
read -p "input test round: " divide  # 每一个N随机测试的次数，最后各项数据取平均值
srcFile="src.tmp"         # 默认临时文件
echo "-----init-----"     # 初始化板块
cprecFile="cp_"${recFile} # 源文件的拷贝文件名称 
if [ $minN -eq 1 ]; then  # 如果N从1开始，则重置信息统计文件statFile
    rm -f $statFile     
    # 并把头信息重定向输入到statFile中
    echo "N,file size,records num,total runs,runs-var,\
    run-build(s),run-build-var,run-merge(s),run-merge-var,\
    total cost(s),total-var,state" > $statFile
fi
# 为了防止编译环境不同导致的程序运行错误，对辅助程序进行重新编译
# 由于我这里只是在本地测试就省去以下编译步骤以节省时间
# g++ random_creater.cc -o random_creater.exe
# g++ check_sorted.cc -o check_sorted.exe
# g++ unit.cc -o unit.exe
clear
echo "-----test-----"     # 测试板块
# 主循环：对N从minN到maxN以步长为step进行循环测试
for ((N=$minN; N<=$maxN; N+=$step))
do
    # 强制删除每次测试产生的临时文件以及排序文件，只留下信息统计文件以保证测试所占用内存的大小
    rm -f $srcFile $recFile $cprecFile
    # 次循环：针对每个N，测试divide次，最后的结果用unit.exe进行平均处理
    for ((round=1; round<=divide; round++))
    do
        echo "N: $N: round: $round"           # 终端中显示当前测试进度
        ./random_creater.exe $recFile $N      # 产生随即数据
        ./extsort.exe $recFile $srcFile       # 将该次排序的统计信息写入临时文件
        ./check_sorted.exe $recFile $srcFile  # 将该次排序的检查结果写入临时文件
    done
    ./unit.exe $srcFile $statFile    # 针对多次测试产生的临时文件进行均值处理写入统计文件
    rm -f $srcFile                   # 删除临时文件
done
rm -f $cprecFile $recFile            # 测试结束后删除除统计文件外的程序产生文件
########### 测试结束 ############

其中statFile中的头信息为：

N	file size(M)	records num	total runs	runs-var	run-build(s)	run-build-var	run-merge(s)	run-merge-var	total cost(s)	total-var	state
N	文件大小	数据记录个数	产生顺串个数	顺串个数方差	建立顺串耗时	建立顺串耗时方差	归并顺串耗时	归并顺串耗时方差	总耗时	总耗时的方差	sorted/unsorted

单点测试

有了完整的测试逻辑，我们来测试一个N的值来看看效果：

最后我们用EXCEL打开STAT.csv文件，得到：

N=1的测试10次的结果就很显然了，总耗时为0.0083 s。

测了个最小的，那为什么不测一个大的呢。

目前为止受限于我计算机硬盘的大小，我最大只测过N=100000即3.05GB规模的文件，结果如下：

$1375.91\text{ s} /60 \approx 22.93 \text{ min}$，也就是花了几乎23分钟。这个结果直观看上去确实太慢了，而我个人也认为这个可以再快一点，由于耗时比较长，所以我没有多次测试，可能在平均条件下3.05GB的耗时可能会稍微好一点。

多点测试

单点测试有很大的不确定性，而且我们也想知道该算法随时间增长的耗时是什么样子的趋势，所以我们可以继续用上面的测试脚本来测试N是一个范围内的所有数值。

1—1859(0.03125mb—58.0938mb)

为了先有个直观的印象，我测了一组N从1到1859的数据，每组N只测了两次取平均值。得到的结果如下：

顺串个数随N的变化趋势

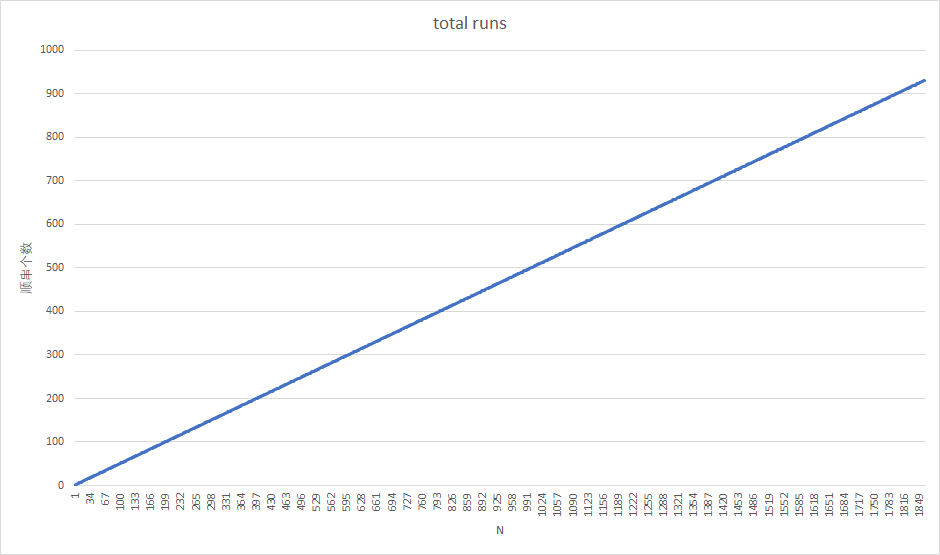
经过线性回归模拟出来的方程为

\[ y = 0.4999x + 1.2492 \]

可以看出斜率$k \approx 0.5$，即说明之前的顺串个数是数据规模的一半(算法分析)
建立顺串耗时、归并顺串耗时、总耗时随N的变化趋势

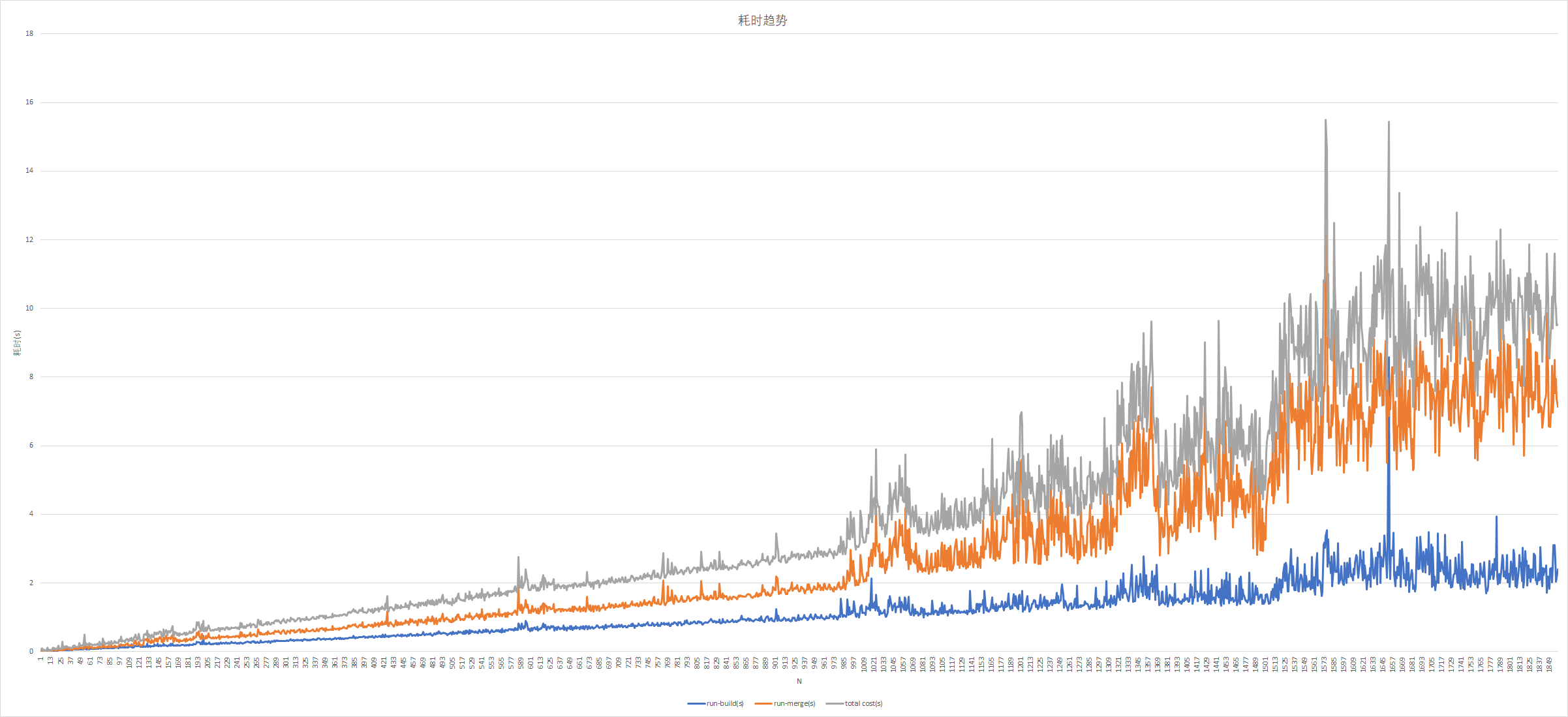
可以很明显的看出在$N>1000$之后各项耗时变得很不稳定，而且显然建立顺串的过程比归并顺串的过程要稳定得多，可能是每组数据测的次数太少导致的。
各指标方差随N的变化趋势

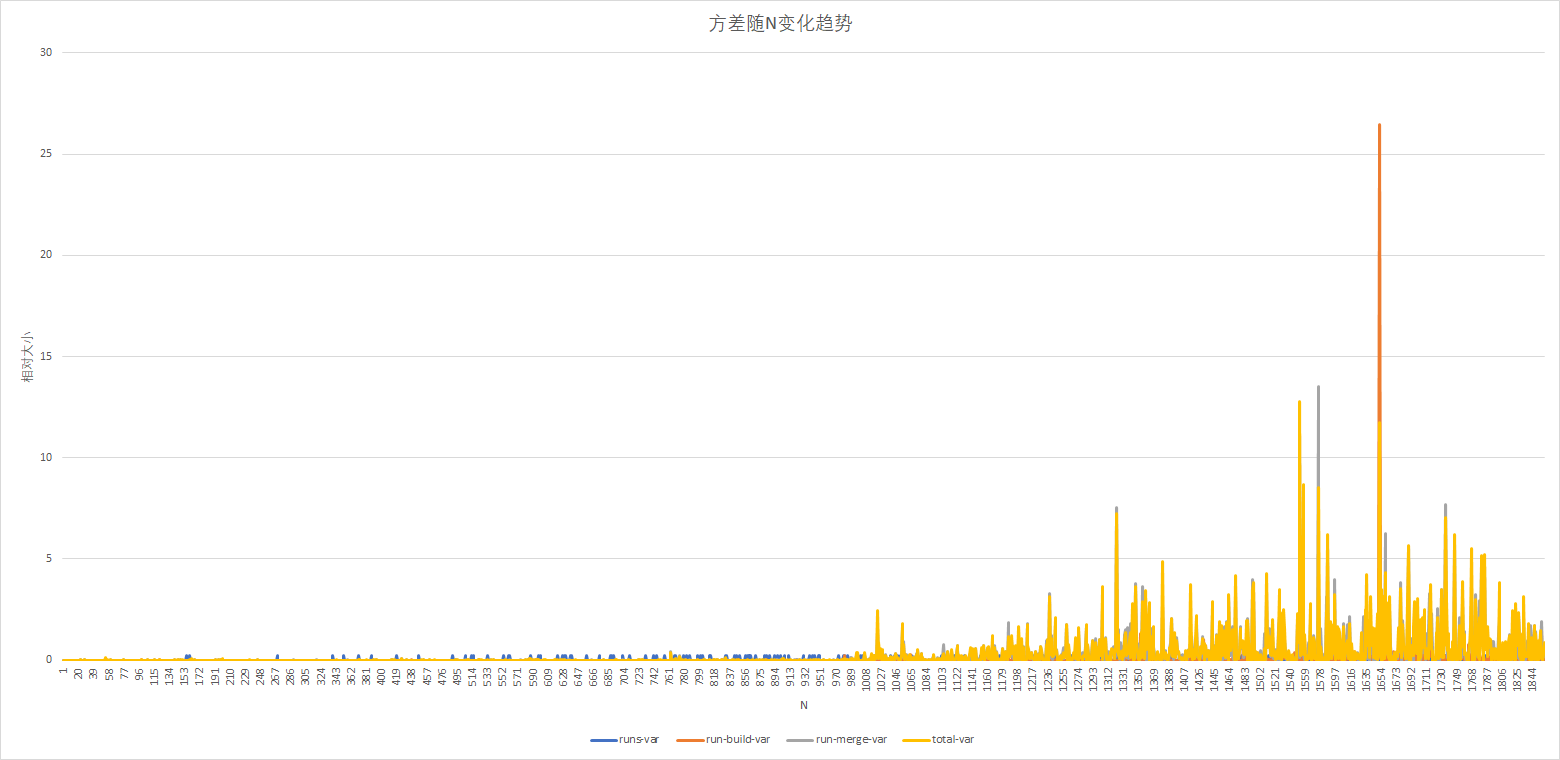
可见随即数据对排序效率影响之大，尤其是在文件较大的时候方差非常不稳定。

1—547(0.03125mb—17.0938mb)

前一种测试结果的数据不是很稳定，在同学的帮助下，我得到了一组N从1到547的数据，其中每组N测100次取平均，应该比上面的结果有更好的说服力。

顺串个数的变化趋势和之前基本相同，这里省略。
建立顺串耗时、归并顺串耗时、总耗时随N的变化趋势

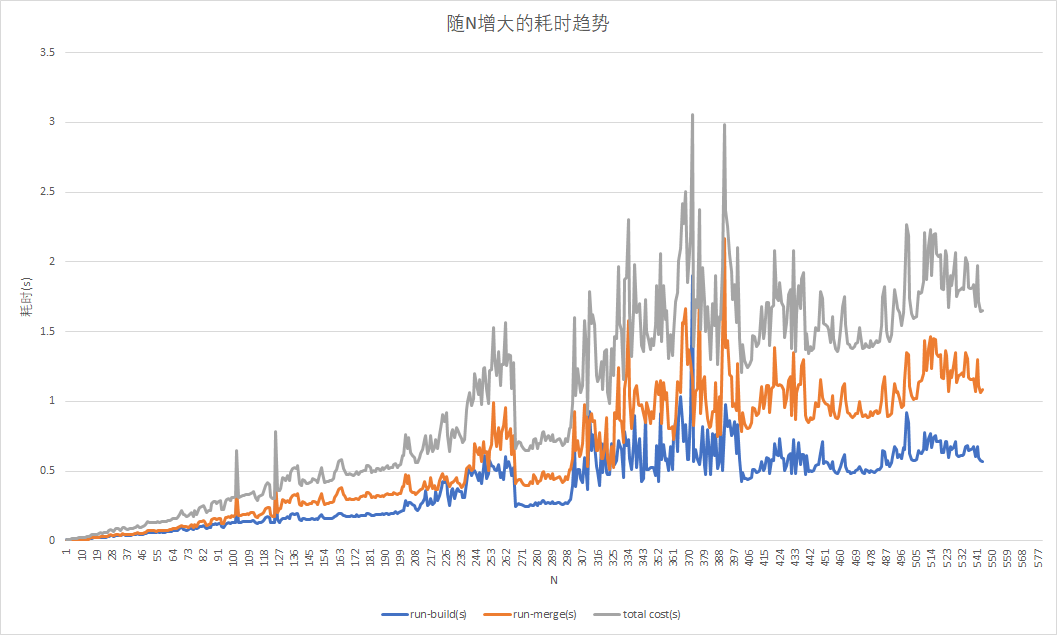
总体上耗时和N的大小是正相关的，不过也N在250到300范围内的耗时出现了明显的断层，这个原因有很多，最有可能的是不同测试环境下的差异造成的，因为我把这些数据分成了很多个数据段分别发给同学们去测试。
各指标方差随N的变化趋势

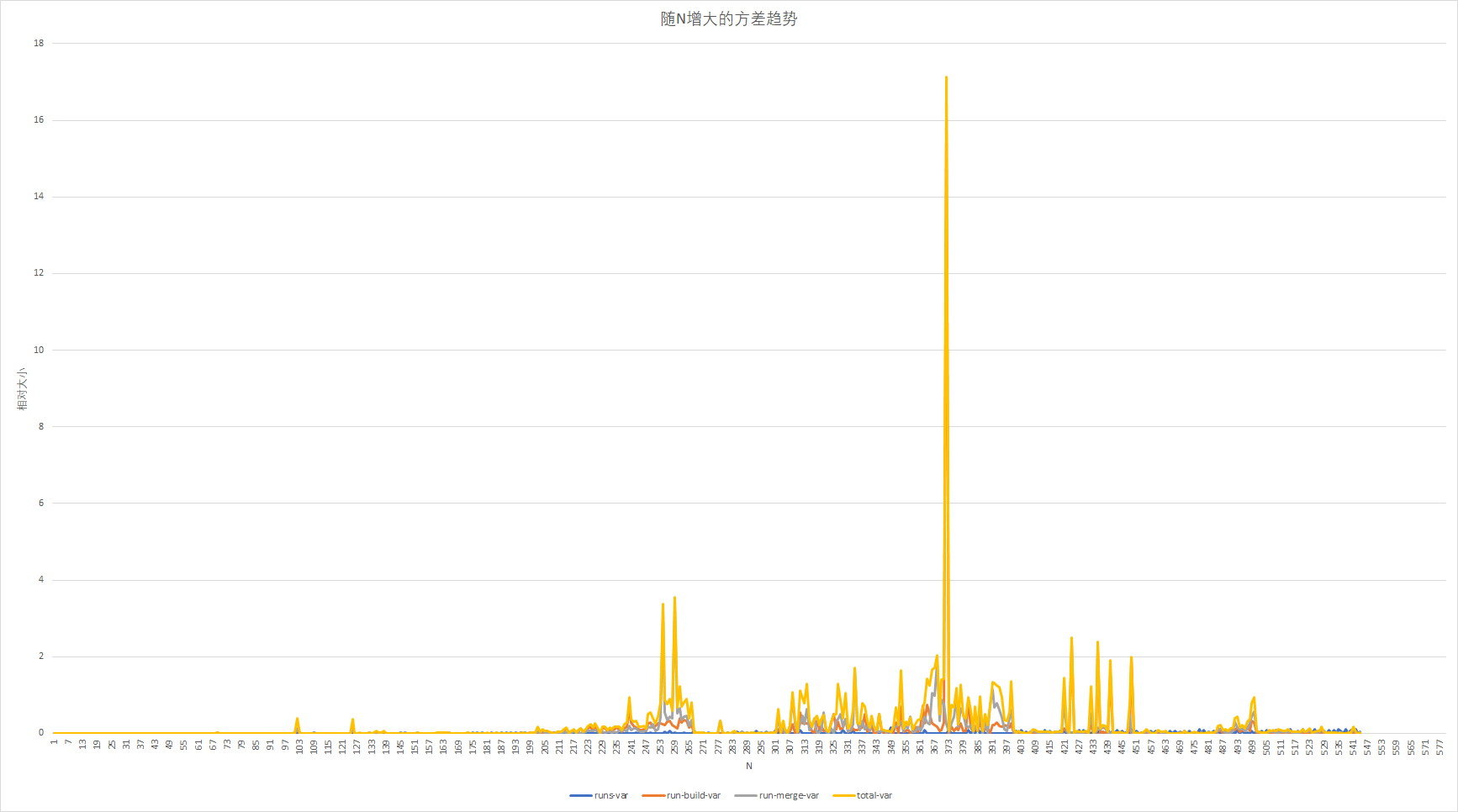
除了N=373左右的那个方差值太大，可能是测试过程有误。其他的方差普遍比较小，也有几处方差比周围大得多的地方。

程序分析

由于我没有找到更合适更快速的测试方法，向上面这样的测试会花费很长时间，所以我也希望从这些数据中总结出一些规律来。

文件中数据的产生是随机的，而这种随机性对排序时间产生的影响是随着N的增大而增大的。第二组测试中每个N测了100次求均值，但是我们还是能明显看出时间消耗的不稳定性。
决定排序时间的因素除了文件初始的随机性之外，还有对文件操作的时间。对单位文件操作的时间会因为不同的硬件环境而改变。程序中操作的文件在逻辑上是连续的但是在物理上是不连续的，计算机操作系统中有专门的部件负责文件内存的分配，而内存中文件的离散程度也会随着已有文件的增大而增大，这也增加了文件操作的时间。这也能说明为什么第二组数据中N在250和300范围内和邻接数据有不同，因为这一段数据是我发给同学们的，在他的硬件环境下的文件操作耗时可能更小。
从第一组数据可以看出来，在N不超过一定范围的时候排序的耗时是接近稳定的，而一旦超过了这个范围，排序的耗时情况便不再那么有序，而对应的方差也明显变大。也就是说，这个排序程序实在一定范围内使用效果比较好，而超出这个范围也可以用，不过耗时可能便不那么容易预测。

当然有了问题就要寻找解决优化的思路。

在N小于一定范围时将所有数据都读入主存进行内部排序，减少文件的操作。我测了一下N=1000，即31.25MB的文件，全部读入主存调用头文件algorithm中的std::sort函数进行快速排序，同样测100次取平均数，得到的结果为2.78071 s，要略小于外部排序的3.0785 s。
由第一组测试图表可以看出，对总耗时影响最大的是归并的部分，所以我们可以针对顺串归并做一些优化。比如在主存允许的情况下采用更多路的归并，减少归并的次数。也可以优化查找最小值的办法，因为查找操作会重复非常多次，我们可以设法维护一种数据结构来实现快速查找多个元素的最小值：最小堆，BIT等数据结构。
对于顺串的建立部分可以想办法在置换选择算法的基础上针对特殊情况进行改进，使得产生的顺串尽可能少。而产生的顺串可以存在不同的文件中方便归并的操作，不一定要存在一个文件中。

结语

至此，我比较详细的描述了外部排序的一种算法的实现以及其性能的测试，也提出了一些改进的拙见。当然文章中算法部分的内容是参考了Clifford A. Shaffer的数据结构与算法分析(C++版)(第三版)英文版中8.5 External Sorting的内容，我没有在网上找到该书原版的电子版，中文版倒是有，不过看过一点觉得翻译的质量并不高，所以希望大家有精力还是能够看一下这本书，这可能是我第一本一个词一个词啃了大半本的英文书了。

特别感谢

由于近期大家都在进行期末的备考，我也是终于有了大把的时间来做一些项目写一些内容。就这个题目而言，真正花费时间的不是程序的编写，而是数据的测试。曾经有连续三天的时间我几乎都在反复测试程序的性能，但到最后发现测试的脚本有问题，所以为了节省时间，我把测试的数据范围分成了很多小份，分别发给了同学进行测试，所以在这里感谢给我提供帮助的同学：

        <input type="checkbox"  checked="checked"><em>Weijun-Lin</em> (<a

href="https://github.com/Weijun-Lin">Github)

        <input type="checkbox"  checked="checked"><em>Marikruz</em> (<a

href="https://github.com/Marikruz">Github)

        <input type="checkbox"  checked="checked"><em>KIIIKIII</em> (<a

href="https://github.com/KIIIKIII">Github)

题外话

说到这次的题目是我们DSAA课程lab3的第二个问题，该课的任课老师也是我的班主任，所以我也是对这门课格外上心，老师也非常负责，除了布置作业之外也给我们布置了三次lab。每次lab只有三四道实验题目，虽然我们有专门的数据结构实验课，但是显然，那个实验课的实验题目要比这个理论课的lab难度要小的多(至少我这么认为)。我还有另一篇文章是写了数据结构实验课的一个题目内容，不过文章的重点显然不在Huffman编码算法上，详细的见Huffman编码压缩文件时的文件储存结构。

而DSAA理论课的lab确实给我留下了一些比较深的印象，我也确实从里面学到了一些东西。比如lab2里的Decision Tree(这是当时我的实验报告，主要就是看一下题目)，虽然这很难说是机器学习的入门，不过写过决策树之后直接给了我很大的信心去攻克了全连接神经网络的算法并在期末考试前完成了全连接神经网络手写体数字识别的项目(Handwritten-digit-recognition-CPP)。还有就是这次的外部排序，虽然这可能并不是考试的重点，但他确实是让我学到了一些关于内存和主存缓冲区方面的内容，更重要的是锻炼了我程序设计和实现的能力。

每次的lab程序都需要在课堂上上台展示，这次的外部排序我也是代表小组去展示，但是演示程序的时候忽略了一点，导致测试N为1000规模的时候竟然跑了40多秒，现在的测试结果是3秒左右，而跟我们组竞争的小组他们的测试耗时也远小于40秒，这我也觉得很是尴尬，明明同样的算法思路居然效果差这么多。而到后来我才知道原因，因为我是用VS2017编译得到的可执行文件，在编译的时候一直用的Debug模式，这种条件下编译器不会对程序进行任何优化，而且会保存所有的调试信息以便进一步调试，而选择Release模式后编译，编译器会自动把程序优化，省去调试细节可以实现最好的效果。在Release下编译后程序不知道快了多少倍，这是展示几周之后同学告诉我的，也很遗憾当初没有用最好状态的程序进行演示。而更遗憾的是，当初展示的时候我几乎没有做多点测试，更没有做出图表这样可视化的变化趋势，所以连性能的分析也没有，明明我当时有时间去做但是就没想到。以后有这样的事情我就争取能做的更好吧。

#C++ #算法

外部排序及性能测试

https://blog.scubot.com/article/409/

作者

贺翔/CarOL

发布于

2019年1月12日

许可协议

简单疏散模型(2019美赛) 上一篇

基本空间向量搜索引擎理论(译) 下一篇