快速反平方根算法

什么是反平方根

反平方根即平方根的倒数：

\[ y = \frac{1} {\sqrt x} \]

该计算表达式在图形学中的向量正规化中经常用到，对于大规模场景的法线向量计算，如果仅使用

1
2
3
4
5
float rsqrt(float number)
{
	float y = 1 / sqrt(number);
  	return y;
}

就显得非常笨拙。

因为在计算机中，一般加法与乘法都是经过硬件优化的，计算速度会很快，求平方根则不同。

为了更快的计算一个浮点数的平方根的倒数，一个更快更奇怪的算法在《雷神之锤3》中被提出（可能更早），该算法也成为了Magic Number的典型案例。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
float Q_rsqrt( float number )
{
	long i;
	float x2, y;
	const float threehalfs = 1.5F;

	x2 = number * 0.5F;
	y  = number;
	i  = * ( long * ) &y;                       // evil floating point bit level hacking
	i  = 0x5f3759df - ( i >> 1 );               // what the fuck?
	y  = * ( float * ) &i;
	y  = y * ( threehalfs - ( x2 * y * y ) );   // 1st iteration
//y  = y * ( threehalfs - ( x2 * y * y ) );   // 2nd iteration, this can be removed

	return y;
}

要理解该算法是如何工作的，我们需要掌握一些内容：

  1. 浮点数在计算机内存中的存储方式
  2. c语言中的类型转换与重解释
  3. 牛顿迭代法（求函数的近似零点）

IEEE 754

在IEEE 754标准中，定义了浮点数在计算机中的存储方式：

以32位浮点数为例（在c语言中为float）

其中32位bit被分割成了3部分（科学计数法）：

  1. Sign 符号位，0为正数，1为负数。
  2. Exponent 指数位，简写为\(E\)，一共包含8位bit。
  3. Fraction 或 Mantissa 尾数位，简写为\(M\)，一共包含23bit。

对于求反平方根的算法，符号位可以不进行讨论，因为输入的浮点数只有为正该算法才在实数域中有意义。

对于指数位\(E\)（移码），可以表示-126到127（-127和128被用作特殊值处理），实际表示的2的指数应该是\(E-127\)。

对于尾数位\(M\)，表示的是科学计数法中，尾数的小数点后的数字，因为在二进制的科学计数法表示里，尾数的小数点前的数字必为1。

那么，根据IEEE 754的定义，一个浮点数（32位）F就可以表示为： \[ F = (-1)^S \cdot 2^{E - 127} \cdot (1 + 2^{-23}M) \] 在本算法中，符号位可以认为恒0，即可化简为： \[ F = 2^{E-127}\cdot (1+2^{-23}M) \] 同时，如果我们将该32位看作是int或long（在c语言中二者可以看做同一类型），那其对应的整形数\(L\)为： \[ L = 2^{23}E + M \] 对于同样的32位bit，我们可以将其解释为浮点数\(F\)，也可以解释为整数\(L\)。那么\(F\)和\(L\)之间有没有数量上的关系？

\(L\)与\(F\)的关系

对于\(F\)的表达式，我们可以进行这样的运算： \[ \begin{align} F=& 2^{E-127}\cdot(1+2^{-23}M) \\[1ex] \log_2(F)=&\log_2(2^{E-127} \cdot (1+2^{-23}M)) \\[1ex] \log_2(F)=&\log_2(2^{E-127}) + \log_2(1+2^{-23}M)\\[1ex] \log_2(F)=&E-127 + \log_2(1+2^{-23}M) \end{align} \] 观察函数\(f(x)=x\)与\(g(x)=\log_2(x+1)\)

函数图像

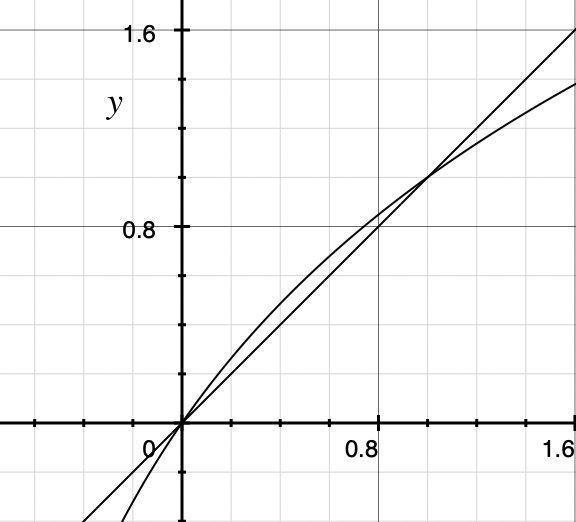
当\(0\le x \le 1\)时，\(f(x)\approx g(x)\)即可表示为\(f(x) = g(x) + \mu\)，其中\(\mu\)为误差。

故\(\log_2(1+2^{-23}M)\approx2^{-23}M + \mu\)，即： \[ \begin{align} \log_2(F) =& E - 127 + \log_2(1 + 2^{-23}M) \\[1ex] \log_2(F) =& E - 127 + 2^{-23}M + \mu \\[1ex] \log_2(F) =& 2^{-23}(2^{23}E + M) + \mu - 127 \end{align} \] 又因为\(L=2^{23}E + M\)，得 \[ \log_2(F) = 2^{-23}L + \mu - 127 \] 至此，我们得到了对于同一32位二进制串的浮点数解释\(F\)与整数解释\(L\)之间的近似数量关系。

c语言中的类型转换与重解释

Type punning (类型双关): c++中可以使用reinterpret_cast实现双关

在c语言中，如果我们需要将32位浮点数float转为long（或int），我们可以显示得：

1
2
float num_float = 3.3;
long num_long = (long)num_float;

得到的结果num_long为3。

但是如果我们更底层的，对于IEEE 754中提到的，我想把32位浮点数，转换成32bit都相同的整形，该如何做呢？

在程序运行中，变量的数据一般是存储在内存中，在c语言里可以通过&来获取变量的地址。而(long *) 地址即可使用long的指针指向该地址，再使用*获取该指针的内容，即可实现了在c语言里使用指针重解释内存中的数据类型。

即Q_rsqrt函数中的i = * ( long * ) &y;，y本为float类型，使用该方法可以将其bit不变得解释为long类型的i变量。

求解反平方根的近似

在求解之前，我们先回顾上面的结论： \[ \begin{align} \log_2(F) = 2^{-23}L + \mu - 127 \end{align} \] 其中\(F\)为32位bit的浮点数解释，\(L\)为32位bit的整形解释。而在c语言中使用指针可以实现\(F\)与\(L\)的转换，更重要的是，转换是极快的。

至此，我们可以明确快速平方根的算法的目的：

  1. 求解有效32位浮点数的平方根的倒数
  2. 尽可能的只使用加法、乘法与位运算
  3. 时间复杂度为常数
  4. 可以有一些误差（计算机存储浮点数本身就有误差）

值得注意的是，浮点数本身不支持位运算

回到一开始的问题，求解：\(y=1/\sqrt x\)

问题可以表示为： \[ F_y = 1 / \sqrt{F_x} \]

\[ \begin{align} F_y =& 1 / \sqrt{F_x} \\[1ex] \log_2(F_y) =& \log_2(1/\sqrt{F_x}) \\[1ex] \log_2(F_y) =& \log_2(F_x^{-1/2}) \\[1ex] \log_2(F_y) =& -\frac{1}{2}\log_2(F_x) \end{align} \]

将\(\log_2(F) = 2^{23}L + \mu - 127\)带入上式： \[ \begin{align} \log_2(F_y) =& -\frac{1}{2}\log_2(F_x) \\[1ex] 2^{-23}L_y + \mu - 127 =& -\frac{1}{2}(2^{-23}L_x + \mu - 127) \\[1ex] 2^{-23}L_y =& -\frac{1}{2}(2^{-23}L_x + 3\cdot(\mu - 127))\\[1ex] L_y=& \frac{3}{2}\cdot2^{23}\cdot(127 - \mu) -\frac{1}{2}L_x \end{align} \] 对于上式结果：\(L_y=\frac{3}{2}\cdot 2^{23} \cdot (127 - \mu) - \frac{1}{2} L_x\)

\(F_x\)表示32位bit的\(x\)的浮点数表示，\(L_x\)表示32位bit的\(x\)的整形表示。在c语言中，二者是可以互相转换的。

前半部分：\(\frac{3}{2}\cdot 2^{23}\cdot (127-\mu) = \mathrm{0x5f3759df}\)，在\(\mu=0.04505\)时成立，更通用的，可以使\(\mu=0.0430\)。

后半部分：\(-\frac{1}{2 }L_x\)在c语言中可以使用位操作实现：-(Lx >> 1)

故使用c语言实现该表达式为：

1
long Ly = 0x5f3759df - (Lx >> 1);

即原算法实现中的内容。

通过该公式可以求出\(L_y\)，再在c语言中通过Fy = * (float *) &Ly即可求得\(F_y\)。

牛顿迭代

在上述推导中，我们用到了\(\log_2(x+1) \approx x + \mu\)。

一般情况下\(\mu=0.0430\)，该算法实现中取了\(\mu=0.04505\)。都是为了使用\(x+\mu\)逼近\(\log_x(x+1)\)。

虽然误差总是不可避免，为了减少这种逻辑上带来的误差，我们需要将误差尽可能的减少。

牛顿迭代法是一种用来近似函数零点的方法：

牛顿迭代

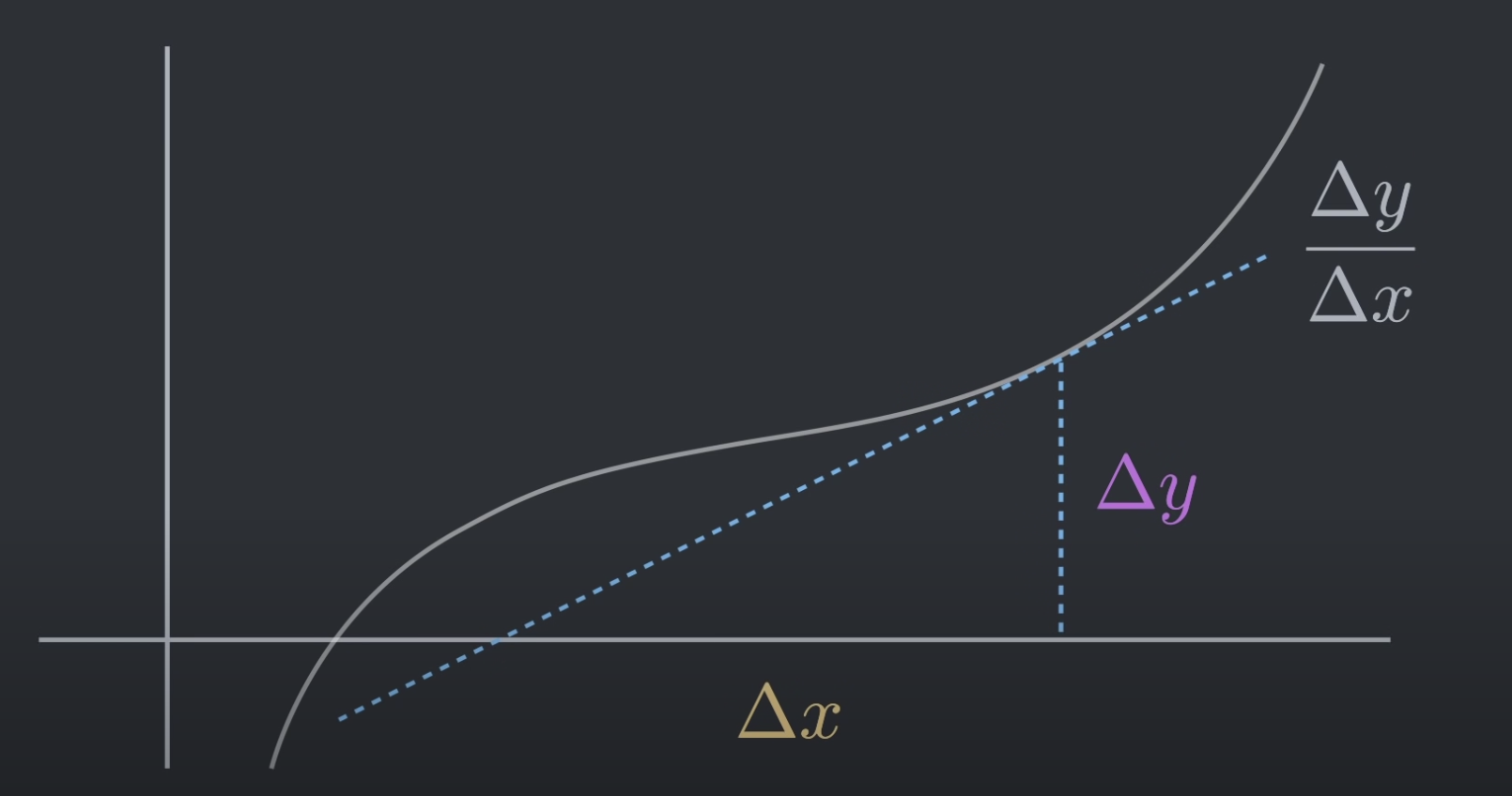
对于某复杂函数，我们无法推导出其零点的表达式，或者零点的表达式不利于计算机的计算，我们就可以使用牛顿法来近似得到零点。

牛顿法的核心思想是：切线是曲线的线性逼近

对于某一可导函数，我可以取其定义域内的任意\(x\)：

  1. 在函数上对应\(x\)的位置求一阶导数，即函数在\(x\)位置的切线。
  2. 该切线与X轴最多有一个交点，如果有交点的话，我们就以该交点为\(x\)重复求切线，求切线与X轴交点的这个过程。

每次求的切线与X轴的交点都更加逼近函数的真正零点。

根据上图，容易得到： \[ \begin{align} \Delta x =& \frac{\Delta y}{\frac{\Delta y}{\Delta x}} \\[1ex] \Delta x =& \frac{f(x)}{f^\prime(x)} \\[1ex] x_{new} =& x - \frac{f(x)}{f^\prime(x)} \end{align} \] 对于牛顿法求零点，我们需要知道

  1. 函数的表达式
  2. 初始迭代值

所以对于本算法，我们需要构造\(y\)的函数，使得其零点为\(y=\frac{1}{\sqrt x}\)。

经过一些变换，我们就可以写出该函数： \[ f(y) = \frac{1}{y^2} - x \] 约束\(y>0\)，易得：\(f^\prime(y) = -2 \cdot y^{-3}\)

使用牛顿法的前提：函数表达式我们有了，初始迭代值我们也在上面求出来了\(F_y\)。

那就可以开始进行牛顿迭代的推导： \[ \begin{align} y_{new} =& y - \frac{f(y)}{f^\prime(y)} \\[1ex] y_{new} =& y - \frac{y^{-2} - x}{-2 \cdot y^{-3}} \\[1ex] y_{new} =& y + \frac{1}{2} (y - xy^3) \\[1ex] y_{new} =& y(\frac{3}{2} - \frac{1}{2}xy^2) \end{align} \] 我们可以明确上式中：\(y\)是迭代的值，初识迭代值为\(F_y\)，\(x\)为\(y=\frac{1}{\sqrt x}\)中的\(x\)。

那么就很容易可以转换成c语言中的：

1
Fy = Fy * (1.5 - 0.5 * x * Fy * Fy);

对应源代码中的：

1
y  = y * ( threehalfs - ( x2 * y * y ) );

在该算法过程中，进行一次迭代即可满足精度的需求。

现在我们就可以把原码进行完整的解释：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
float Q_rsqrt( float number )
{
	long i;
	float x2, y;
	const float threehalfs = 1.5F;   // 牛顿迭代中的1.5

	x2 = number * 0.5F;
	y  = number;
	i  = * ( long * ) &y;                      // 将32bit浮点数y重新解释为32bit整形i
	i  = 0x5f3759df - ( i >> 1 );              // 对i求反平方根的近似
	y  = * ( float * ) &i;                      // 把32bit整形i重新解释为32bit浮点数y
	y  = y * ( threehalfs - ( x2 * y * y ) );  // 第一次牛顿迭代
//y  = y * ( threehalfs - ( x2 * y * y ) );   // 第二次迭代，看起来不需要

	return y;
}

推广到double类型

以上的算法只针对32位浮点数float，对于64位浮点数double我们也可以应用该思想设计出快速的反平方根算法。

在double类型的64位bit中： 1. 符号位占1bit 2. 指数位\(E\) 占11bit 3. 尾数位\(M\) 占52bit

有了这些数据，我们就可以写出c语言中的函数实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
double Q_rsqrt(double number)
{
	long long i;
	double x2, y;
	const double threehalfs = 1.5F;   // 牛顿迭代中的1.5

	x2 = number * 0.5F;
	y  = number;
	i  = * ( long long * ) &y;                       // 将64bit浮点数y重新解释为64bit整形i
	i  = 0x5fdd3020c49ba400 - ( i >> 1 );               // 对i求反平方根的近似
	y  = * ( double * ) &i;                      // 把64bit整形i重新解释为64bit浮点数y
	y  = y * ( threehalfs - ( x2 * y * y ) );   // 第一次牛顿迭代
//y  = y * ( threehalfs - ( x2 * y * y ) );   // 第二次迭代，看起来不需要

	return y;
}

其中0x5fdd3020c49ba400根据\(\mu\)的实际取值不同而不同。

#C++ #C
快速反平方根算法
https://blog.scubot.com/article/39b0/
作者
贺翔/CarOL
发布于
2021年10月10日
许可协议