计算机图形学-着色
概述
本文章用来记录计算机图形学中与 着色(shading) 相关的知识。
着色的定义
在绘画过程中引入明暗或颜色的不同。
"The darkening or coloring of an illustration or diagram with parallel lines or a block of color."
—Merriam-Webster Dictionary
在计算机图形学中,可以理解为:对不同的物体应用不同材质的过程。
基础着色模型
Blinn-Phong光照模型—Blinn-Phong Reflectance Model
Blinn-Phong光照模型认为图像中体现在物体上的光分为三部分:
- 高光(Specular highlights)
- 漫反射(Diffuse reflection)
- 环境光(Ambient lighting)

对物体表面的每一个点抽象出以下属性:
- 观察方向 \(\vec v\)
- 该点(局部平面)的法线向量 \(\vec n\)
- 光照方向 \(\vec l\)
- 该点(平面)的参数:颜色、反光系数等
着色操作只考虑物体局部的显示,不将阴影或其他物体考虑在内,即shading \(\not =\) shadow。
下面介绍Blinn-Phong模型中光照的三个部分。
漫反射 Diffuse reflection
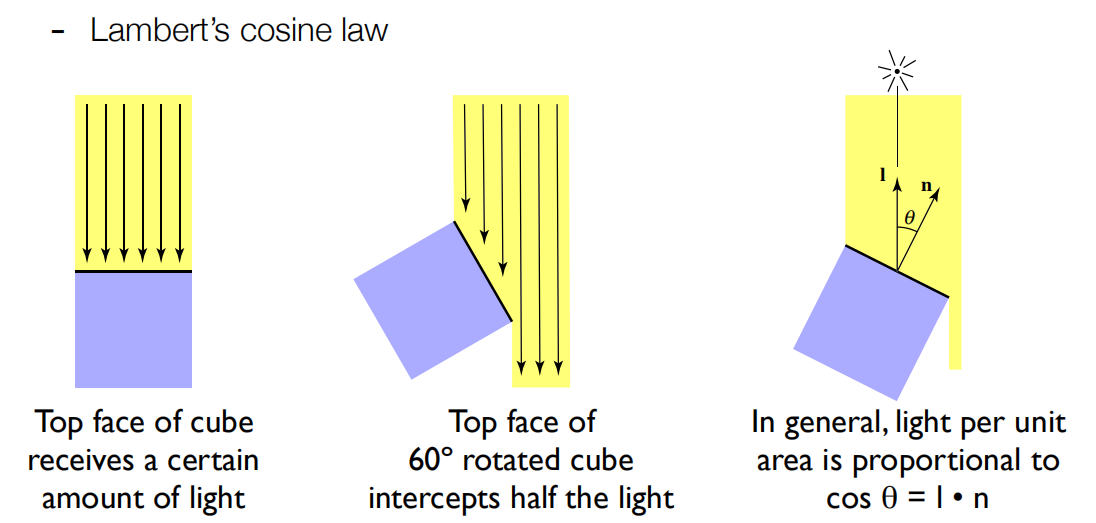
对于漫反射考虑以下因素的影响:
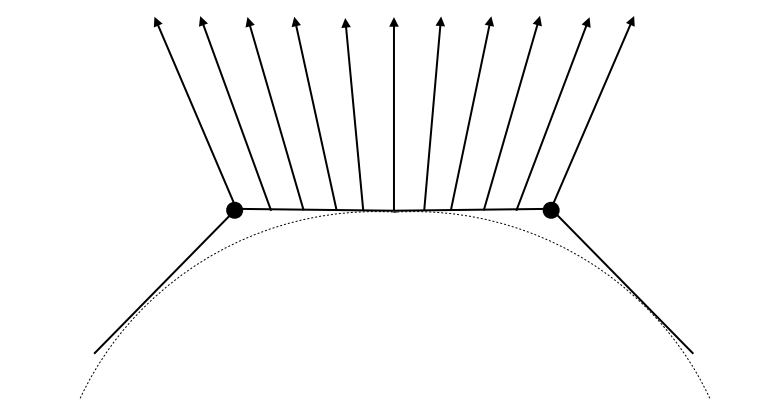
着色点上光的接收
光是一种能量形式,着色点周围单位面积接受到的光能量越大,显示的就应该越亮。
根据上述分析引出 Lambert's 余弦定理:着色点接受到的光照的强度与光照方向和平面法线方向的余弦成正比。
光能量的衰弱
假设点光源在某一时刻发出的光照能量在三维空间中以球壳形式传播且没有能量损耗,那么根据能量守恒,任意时刻球壳上的光的能量总和都应该相等。
根据球面积公式\(S=4\pi R^2\),着色点距离光源\(r\),着色点收到的光能量为\(I\),那么\(I \propto 1/r^2\),即光照强度与离光源的距离呈现 平方反比 关系。
这里将光能与光强做等价处理并不严谨,不过鉴于Blinn-Phong本身就是个简化模型,就不多考虑其中的问题。
根据上面两点可以写出着色点的漫反射光照强度表达式:
\[ L_d = k_d(I/r^2)\max(0, \vec n \cdot \vec l) \]
其中:\(L_d\) 为着色点的漫反射光照强度,\(k_d\)为漫反射参数(颜色等),\(I\) 为光源处光照强度,\(r\) 为着色点到光源处距离。
解释:
- \(\vec n \cdot \vec l\) 如果为负数,则认为该点不被照亮(不考虑折射等)。
- \(k_d\)表示为单个小数时表示物体的光反射率,影响物体的亮暗程度;如果将\(k_d\)表示为向量即可表示物体对不同颜色的反射率,影响物体的颜色。
- \(L_d\)的表达式中没有观察方向\(\vec v\)的参与,因为模型中假设了某点的漫反射总是均匀的,不管从哪个角度观察都能看到同样的漫反射效果,故与\(\vec v\)无关。
- 表示方向的向量:\(\vec n\),\(\vec v\)和\(\vec l\)都是单位向量。
漫反射示例:

高光 Specular highlights
假设光照在物体的局部平面发生镜面反射,镜面反射的光线方向是\(\vec R\),那么如果观察方向\(\vec v\)与\(\vec R\)接近时会观测到高光。
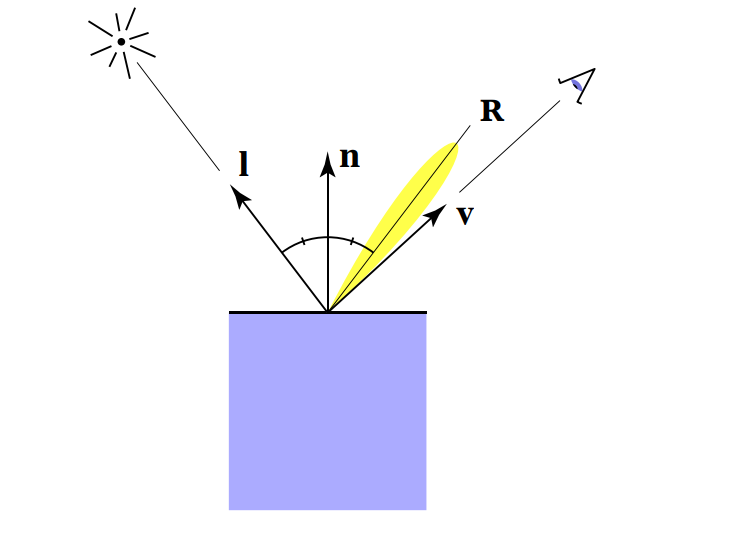
\(\vec R\)的计算比较麻烦,Blinn-Phong模型中引入半程向量(half vector)来解决这个问题。
如果\(\vec v\)与\(\vec R\)很接近,那么\(\vec n\)与\(\vec l\)和\(\vec v\)的角平分线的方向向量很接近,定义半程向量\(\vec h\)为\(\vec l\)和\(\vec v\)的角平分线方向的单位向量:\(\vec h = \rm{bisector}(\vec v, \vec l) = \frac{\vec v + \vec l}{\mid \mid \vec v + \vec l \mid \mid}\)
推导\(\vec R=(X_R, Y_R, Z_R)\): \[ \begin{align*} \frac{\vec R + \vec l}{\mid \mid \vec R + \vec l \mid \mid} &= \vec n \\[2ex] \begin{pmatrix} \frac{X_l + X_R}{\sqrt{(X_l + X_R)^2 + (Y_l + Y_R)^2 + (Z_l + Z_R)^2}} \\ \frac{Y_l + Y_R}{\sqrt{(X_l + X_R)^2 + (Y_l + Y_R)^2 + (Z_l + Z_R)^2}} \\ \frac{Z_l + Z_R}{\sqrt{(X_l + X_R)^2 + (Y_l + Y_R)^2 + (Z_l + Z_R)^2}} \end{pmatrix} ^\top &= (X_n, Y_n, Z_n) \end{align*} \] 可以列出三个等式,求三个分量,计算量太大不继续算了。
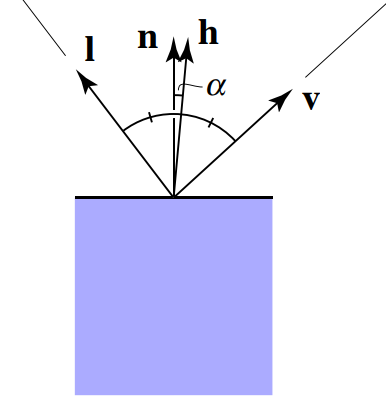
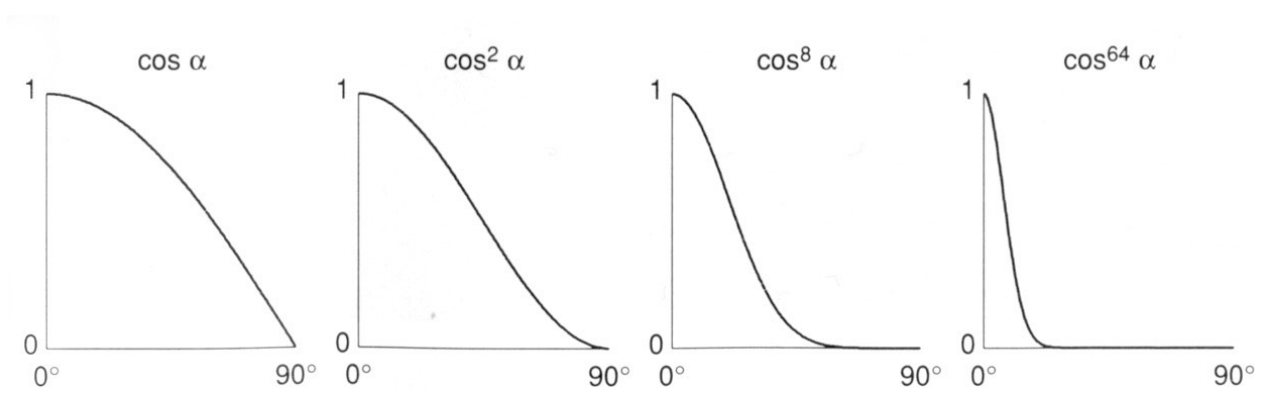
可以写出着色点的高光亮度表达式: \[ \begin{align*} L_s &= k_s(I/r^2) \max (0, \cos \alpha) ^ p \\ &= k_s(I/r^2) \max(0, \vec n \cdot \vec h) \end{align*} \] 其中\(L_s\)为着色点的高光亮度,\(k_s\)为高光反射系数, \(p\)表示高光敏感度。
解释:
Blinn-Phong光照模型中使用\(\vec n\)与\(\vec h\)来表示高光角度,Phong光照模型中使用\(\vec R\)与\(\vec v\)来表示高光角度。
用指数\(p\)来表示可以产生高光的角度区间(敏感程度),\(p\)越大,能看到高光的角度就越小:
漫反射+高光示例:

环境光 Ambient lighting
真实的环境光照很复杂,Blinn-Phong模型做了一个大胆的假设:所有着色点的环境光照均相同: \[ L_a = k_a I_a \] 其中:\(L_a\)为着色点环境光的光照强度,\(k_a\)是环境光反射系数, \(I_a\)为环境光强度常数。
解释:
- 在这个模型中环境光与观测方向和光照方向均无关。
- 可以将环境光理解成物体本来的颜色,使得不是所有地方都是黑色的。
- 精确地计算需要利用到环境光照的知识(不在本文章)。
模型效果
将以上三种光照效果加在一起,就可以得到某一着色点的光照强度: \[ \begin{align*} L &= L_a + L_d + L_s \\ &= k_a I_a + k_d(I/r^2 )\max(0, \vec n \cdot \vec l) + k_s (I /r^2) \max(0, \vec n \cdot \vec h) ^ p \end{align*} \] 效果:

着色频率
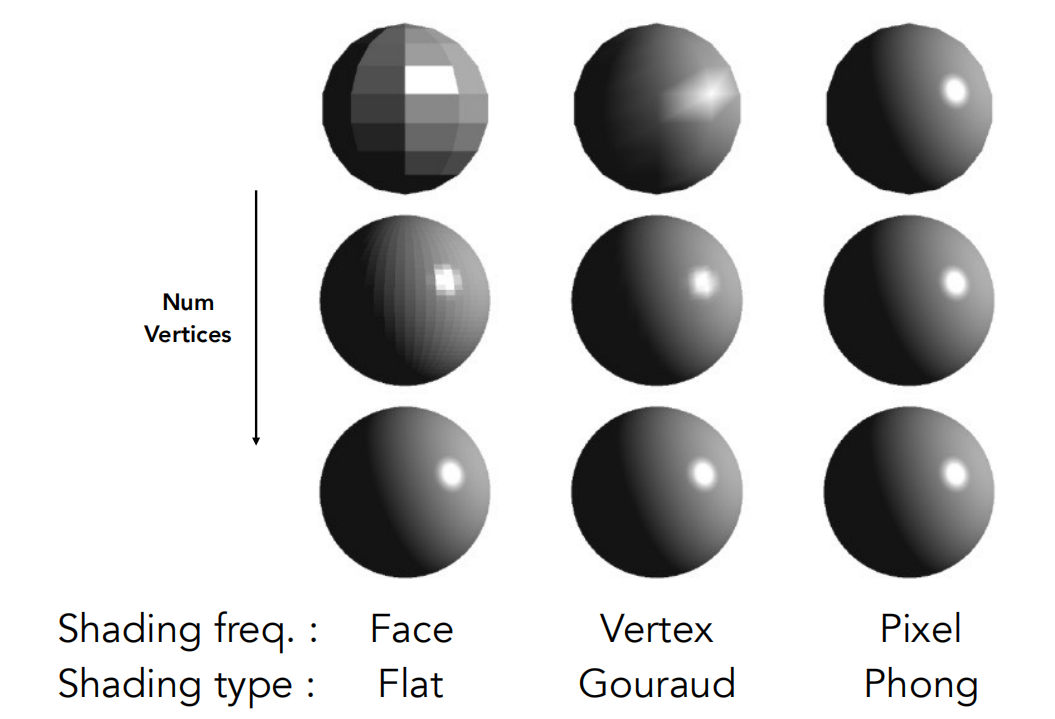
三种不同的着色方式:
Flat shading:以一个三角形为单位,三角形内部颜色不变化,只针对三角形一个点做着色处理就可以对三角形中所有点应用。(逐三角形)

Gouraud shading:对三角形三个顶点求出其法线向量,并算出三个顶点的着色情况,再在三角形内部对三个顶点的颜色做插值。(逐顶点)
关于顶点的发现向量计算:顶点法线向量

Phong shading:对三角形三个顶点求出其法线向量,对三角形内部每个点插值出对应的法线,对每一个像素进行着色。(逐像素)
Phong shading是一种着色频率,与Blinn-Phong着色模型不是一个概念。
关于像素的法线插值:像素法线插值

当模型足够复杂(顶点数量足够多时),Flat shading的效果不一定比Phong shading(计算量大)差。而当模型过于复杂时,顶点数量多余屏幕像素数量,则Flat shading的计算量比Phong shading还要大,具体采取什么样的着色频率要根据实际情况考虑。
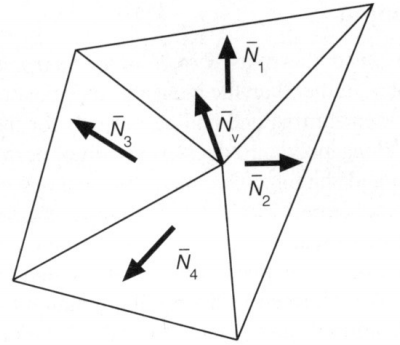
顶点法线向量
任何一个顶点都与周围若干个三角形所关联,可以简单的认为该点的法线向量是周围三角形的法线向量的平均:
 \[
\vec N_v = \frac {\sum_i \vec N_i}{ \mid \mid \sum_i \vec N_i \mid \mid}
\]
\[
\vec N_v = \frac {\sum_i \vec N_i}{ \mid \mid \sum_i \vec N_i \mid \mid}
\]
改进:认为每个三角形面积越大权重越大,取得法线的加权平均,效果更好。
像素法线插值
使用重心坐标(Barycentric interpolation)插值,后归一化每个向量。详细的插值方法见后续。